已写下 85 篇博客文章,共计 101,765 字,完整阅读预计需要 8.5 小时,已有 1,860,186 次阅读。
按照【分类】筛选文章
按照【标签】筛选文章
【教女朋友 从 0 到 1 学编程系列】三、2048 前端游戏实战

【教女朋友 从 0 到 1 学编程系列】二、快速掌握前端基础
首先明确一点学习的最根本原则: - 预习:是不可能预习的 - 复习:是不可能复习的 那么如何能够教女朋友快速从零基础上手写代码,将成为本课时的最关键内容。 前端的基础主要包括三个部分,HTML、CSS、JS,其中 HTML 和 CSS 是前端的基础,JS 是前端的核心。本课时主要讲解 HTML 和 CSS,JS 将在下一阶段重点讲解。 简单来说,HTML 是网页的骨架,CSS 是网页的皮肤,JS 是网页的灵魂。 ## HTML HTML 指的是超文本标记语言: **H**yper**T**ext **M**arkup **L**anguage 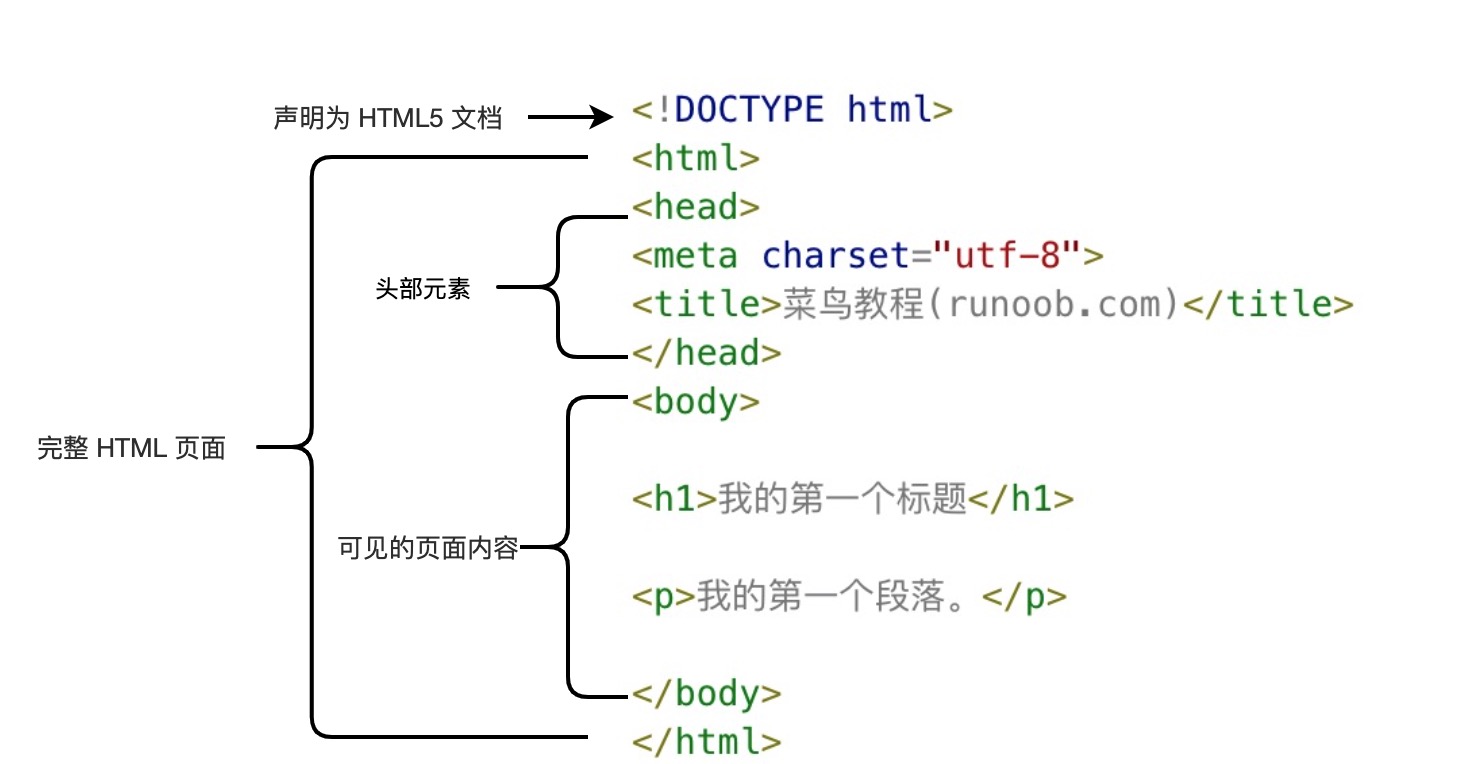 > 图片来自 [Runoob.com](https://www.runoob.com/html/html-intro.html) ### 通用声明 HTML 5: ```html <!doctype html> ``` 目前最常见的也是最简单的声明方式,其他还有 html 4.01、 xhtml 1.0 等,具体可以参考: [https://www.runoob.com/tags/tag-doctype.html](https://www.runoob.com/tags/tag-doctype.html) (`可以忽略不看`) 目前在大部分浏览器中,直接输出中文会出现中文乱码的情况,这时候我们就需要在头部将字符声明为 `UTF-8` 或 `GBK`。 整体页面结构: - `DOCTYPE` 声明 - `<html>` 页面元素 - `<head>` 头部信息元素(不会显示,内部元素顺序可以随意调整) - `<title>` 页面标题 - `<meta>` 元数据 - 其他头部信息 - `<body>` 网页主体 - 各元素内容 示例代码: ```html <!doctype html> <html lang="zh-CN"> <head> <meta charset="utf-8" /> <title>页面标题</title> </head> <body> <h1>我的第一个标题</h1> <p>我的第一个段落。</p> <!-- 这是一段注释,不会显示到页面中 --> </body> </html> ``` > [在线体验](https://www.runoob.com/try/try.php?filename=tryhtml_headers) ### head 元素 | 标签 | 描述 | | :

【教女朋友 从 0 到 1 学编程系列】一、计算机基础
教女朋友 从 0 到 1 学编程系列大纲,主要技术栈围绕 JS/TS 前后端,欢迎完善补充,提出宝贵意见。

Promise、async/await 使用经验
# Promise 产生:改善 Callback Hell 问题 ## 什么样的方法可以用 Promise 重写 例 1: ```javascript mysql.query('SELECT 1 + 1 AS solution', function (err, rows, fields) { if (err) { throw err; } // 对查询结果进行操作 console.log('The solution is: ', rows[0].solution); }); ``` 例 2: ```javascript fs.readFile('myfile.txt', function (err, file) { if (err) { throw err; } // 对file进行操作 }); ``` ## 如何将一个回调方法改为 Promise ### Promisify 一般情况下,该方式首选。 ```javascript const util = require('util'); const fs = require('fs'); const stat = util.promisify(fs.stat); stat('.') .then((stats) => { // Do something with `stats` }) .catch((error) => { // Handle the error. }); ``` ### new Promise() 虽然所有的最终实现原理应该都是这样,但这种写法上的话,又再次出现了地狱回调的问题,可读性非常差。 ```javascript const fs = require('fs'); const stat = (...args) => new Promise((resolve, reject) => { fs.stat(...args, (err, stats) => { if (err) { reject(err); } else { resolve(stats); } }); }); stat('.') .then((stats) => { // Do something with `stats` }) .catch((error) => { // Handle the error. }); ``` ### Defer 兼顾了可读性的一种写法。 ```javascript const fs = require('fs'); const getDefer = () => { const deferred = {}; deferred.promise = new Promise((resolve, reject) => { deferred.resolve = resolve; deferred.reject = reject; }); return deferred; }; const stat = (...args) => { const deferred = getDefer(); fs.stat(...args, (err, stats) => { if (err) { deferred.reject(err); } else { deferred.resolve(stats); } }); return deferred.promise; }; stat('.') .then((stats) => { // Do something with `stats` }) .catch((error) => { // Handle the error. }); ``` ## 如何调用 Promise 方法 ### 直接执行 ```javascript promiseFn() .then() .catch() .then() // 此处的 .then 未经过异常捕获 .finally(); // 不管成功失败,最终都将执行 ``` ### 批量执行 ```javascript Promise.all([promiseFn1(), promiseFn2()]).then(); Promise.allSettled(); // 推荐 Promise.race(); Promise.any(); ```

前端阅读体验优化-GitBook自动换肤

JS 判断一个数是否为 2 的 N 次幂
问题: > 判断一个数(x)是否为 2 的 N 次幂,如果是,返回是 2^n 中的 n,如果不是返回 false 约束: `x <= 2^800` ## SB 青年版 不用说,递归肯定是最 sb 的版本: ```js function power2sb(x, n) { n = n || 0; if (x === 1) { return n; } if (x < 1) { return false; } return power2sb(x / 2, n + 1); } ``` 结果测试: ```js console.log(power2sb(4)); // 2 console.log(power2sb(5)); // false console.log(power2sb(65536)); // 16 console.log(power2sb(Math.pow(2, 52) + 1)); // false console.log(power2sb(Math.pow(2, 53) + 1)); // false 实际结果:53 ``` ## LowB 青年版 低级循环版,与上一个版本半斤八两。 ```js function power2lb(x) { var n = 0; while (x >= 1) { if (x === 1) { return n; } x = x / 2; n++; } return false; } ``` 结果测试: ```js console.log(power2lb(4)); // 2 console.log(power2lb(5)); // false console.log(power2lb(65536)); // 16 console.log(power2lb(Math.pow(2, 52) + 1)); // false console.log(power2lb(Math.pow(2, 53) + 1)); // false 实际结果:53 ``` ## 普通青年版 ```js function power2nm(x) { // 奇数肯定不是2的N次幂 if (x % 2 === 1) { return false; } // 总结规律 // 2^2=4 // 2^3=8 // 2^4=16 // 2^5=32 // 2^6=64 // 2^7=128 // 2^8=256 // 2^9=512 // 所以,个位不可能为 0 if (x % 10 === 0) { return false; } var n = 0; while (x >= 1) { if (x === 1) { return n; } x = x / 2; n++; } return false; } ``` ## 文艺青年版 位运算,无循环。 ```js function power2fs(x) { // 一句话版本 return (x & (x - 1)) === 0 ? (x - 1).toString(2).length : false; /* 解释: 1. (x & ( x - 1)) === 0 先来寻找一下规律: 2^2=4 对应二进制为 100 2^3=8 1000 2^4=16 10000 所以, 2^N=1+N个0 2^N-1=N个1 100 & 11

js版 Leetcode Single Number

js版 Leetcode接受率最低题valid-number

js版Leetcode第一难题wildcard-matching

js版 Leetcode spiral-matrix-ii

API接口性能统计之平均响应时间算法

日本雅虎程序员跳槽程序测试问题